 Image credit: SID
Image credit: SID
Abstract
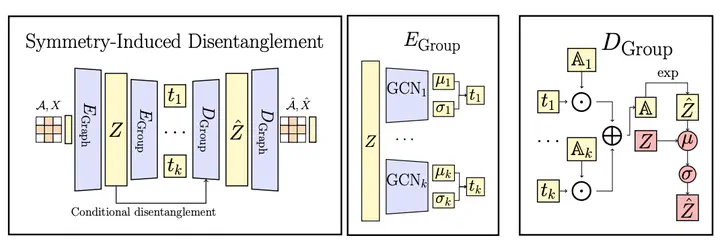
Learning disentangled representations is important for unraveling the underlying complex interactions between latent generative factors. Disentanglement has been formalized using a symmetry-centric notion for unstructured spaces, however, graphs have eluded a similarly rigorous treatment. We fill this gap with a new notion of conditional symmetry for disentanglement, and leverage tools from Lie algebras to encode graph properties into subgroups using suitable adaptations of generative models such as Variational Autoencoders. Unlike existing works on disentanglement, the proposed models segregate the latent space into uncoupled and entangled parts. Experiments on synthetic and real datasets suggest that these models can learn effective disengaged representations, and improve performance on downstream tasks such as few-shot classification and molecular generation.